【知行晓庄】我的发现：生活中处处有数学——长程作业系列研究展示（三十五）

为全面贯彻落实“双减”政策，更好实现减负增效，促进学生全面发展，深化开展江苏省义务教育教学与课程改革项目《长程作业: 小学实践性学习新样本》研究，南京市晓庄小学组织学生分学科开展了长程作业系列研究。本期推出的主题是“数学与生活”，一起来看看孩子们的发现吧。

蜂巢为什么是六边形

南京市晓庄小学 四（3）班 卢梓涵

研究背景

我家门口有一棵桂花树，秋天的时候会飞来很多蜜蜂，有一天我突然发现树上有一个马蜂窝。为了安全起见，妈妈找来物业师傅处理，蜜蜂都吓跑了，只留下空空的蜂窝。

我鼓起勇气走上前去仔细观察，我发现蜂巢是由一个个六边形组成的，而且这些六边形的排列是有规律的。  

研究过程

我很好奇：蜂巢为什么都是六边形的，而不是圆形或三角形的呢？我查了很多资料，从形状和面积两个方面做了些研究，有如下发现：

一、形状对比

我们分别将几个六边形、圆形、三角形紧密有序地排列在一起，开展对比研究，有了惊奇的收获。

1. 六边形

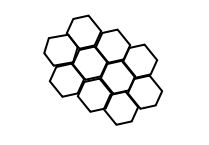
首先，六边形很容易并排堆放，不会影响整个结构的几何形状，这意味着许多蜜蜂可以同时在蜂巢里工作，以便高效地完成酝酿过程。

其次，六边形紧密而整齐地排列在一起，空间的浪费最小，利用率最高。

1. 圆形

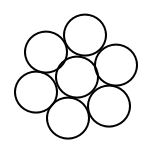
就形状而言，圆形是最方便蜜蜂进出的，但是每两个相邻的圆之间就会留下一个小的空间，这样会造成空间上的浪费，蜂巢的利用率就会降低。

1. 三角形

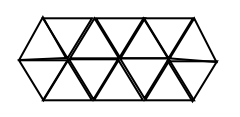
从结构上看，三角形是最稳定的结构，但是三角形不方便蜜蜂进出蜂巢，不方便蜂蜜酝酿。

二、面积计算

我又假设了三种图形的周长都是12cm,计算了它们的面积，如下表：

形状
周长	12cm	12cm	12cm
边长	4cm	3cm	2cm
面积	≈1.73 4×2÷2 =4 ≈ 6.92cm²	3×3=9cm²	≈1.73 ÷4*（2×2）×6 =÷4*4×6 ≈10.38

分析表中数据，我发现：当周长相等时，六边形的面积最大。

研究结论

其实，科学家们研究发现，如果蜂巢呈圆形，会出现空巢；如果是三角形，面积会减小。而这种可容纳高达上万只蜜蜂居住的正六边形的蜂巢，可使用的空间最大，且蜂巢的构造非常精巧，由无数个大小相同的正六边形房孔组成，每个房孔都被其他房孔包围，两个房孔之间隔着一堵蜡制的墙，房孔的底既不是平的，也不是圆的，而是尖的，由三个完全相同的菱形组成。这样蜜蜂们就可以自由进出，而且能储存更多的蜂蜜。不得不说，小蜜蜂真是一个伟大的建筑师和数学家。

数学就在生活中，只要善于观察、勤于思考，就能发现其中的奥秘。

供稿：教务处

审核：校长室